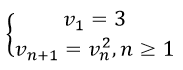Câu 1: Biểu thức nào sau đây cho ta tập giá trị của tổng $S = 1 - 2 + 3 - 4+...-2n + (2n+1)$
-
A. 1
-
B. 0
-
C. n
-
D. n + 1
Câu 2: Giả sử Q là tập hợp con của tập các số nguyên dương sao cho
(a)$ k∈Q$
(b) $n∈Q⟹n+1∈Q,∀n≥k.$
-
A. Mọi số nguyên dương đều thuộc Q
-
B. Mọi số nguyên dương lớn hơn hoặc bằng k đều thuộc Q
-
C. Mọi số nguyên bé hơn k đều thuộc Q
-
D. Mọi số nguyên đều thuộc Q
Câu 3: $∀n∈N∗$ thì chia hết cho:
-
A. 13
-
B. 6
-
C. 8
-
D. 5
Câu 4: Với mọi số nguyên dương n thì $S_{n}=n^{3}+2n$ chia hết cho
-
A. 3
-
B. 2
-
C. 4
-
D. 7
Câu 5: Với mọi số nguyên dương n, tổng $S_{n}=n^{3}+11n$ chia hết cho:
-
A. 6
-
B. 4
-
C. 9
-
D. 12
Câu 6: Với mọi số nguyên dương n, tổng $S_{n}=4^{n}+15-1$ chia hết cho:
-
A. 4
-
B. 6
-
C. 9
-
D. 7
Câu 7: Với mọi số nguyên dương n, tổng $S_{n}=3^{2n}-1$ là:
-
A. 6
-
B. 3
-
C. 12
-
D. 8
Câu 8: Mạnh cầm một tờ giấy và lấy kéo cắt thành 7 mảnh sau đó nhặt một trong số bảy mảnh giấy đã cắt và lại cắt thành 7 mảnh. Mạnh cứ tiếp tục cắt như vậy. Sau một hồi, Mạnh thu lại và đếm tất cả các mảnh giấy đã cắt. Hỏi kết quả nào sau đây có thể xảy ra?
- A. Mạnh thu được 122 mảnh
- B. Mạnh thu được 123 mảnh
- C. Mạnh thu được 120 mảnh
-
D. Mạnh thu được 121 mảnh
Câu 9: Cho $x\neq 0$ và $x+\frac{1}{x}$ là một số nguyên. Khi đó với mọi số nguyên dương n, có kết luận gì về $T(n,x)=x^{n}+\frac{1}{x^{n}}$ ?
- A. T(n,x) là số vô tỉ
- B. T(n,x) là số không nguyên
-
C. T(n,x) là số nguyên
- D. Các kết luận trên đều sai
Câu 10: Cho dãy số $(u_{n}):\begin{cases} & \ u_{1}=2 \\ & \ u_{n+1}=nu_{n}\end{cases}$ với mọi $n\geq 1$
Khi đó số hạng thứ 5 của dạy là:
- A.10
-
B.48
- C.16
- D.6
Câu 11: Cho dãy số $(u_{n})=\frac{sin(\frac{n\pi}{3})}{n+1}$ với mọi $n\geq 1$. Khi đó số hạng $u_{3n}$ của dãy $(u_{n})$ là:
- A. $\frac{1}{3n+1}$
- B. $\frac{1}{n+1}$
- C. $-\frac{1}{3n+1}$
-
D. 0
Câu 12: Cho dãy số $(u_{n})=\frac{n^{2}}{3^{n}}$ với mọi $n\geq 1$. Khi đó số hạng $u_{2n} của dãy $(u_{n})$ là
- A. $\frac{2n^{2}}{3^{n}}$
- B. $\frac{4n^{2}}{6^{n}}$
-
C. $\frac{4n^{2}}{9^{n}}$
- D. $\frac{2n^{2}}{6^{n}}$
Câu 13: Dùng quy nạp chúng mình mệnh đề chứa biến $A(n)$ đúng với mọi số tự nhiên $n \geq p$ ( p là một số tự nhiên). ở bước 1 ( bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng:
- A. $n=1$
- B. $n=p$
- C. $n>p$
- D. $n<p$
Câu 14: Dùng quy nạp chúng mình mệnh đề chứa biến $A(n)$ đúng với mọi số tự nhiên $n \geq p$ ( p là một số tự nhiên). ở bước 2 của chứng minh quy nạp ta giả thiết mệnh đề $A(n)$ đúng với $n=k$.
Khẳng định nào sau đây là đúng?
- A. $k>p$
- B. $k \geq p$
- C. $k=p$
- D. $k<p$
Câu 15: khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến $A(n)$ đúng với mọi số tự nhiên $n\geq p$ (p là một số tự nhiên), ta tiến hành hai bước:
-Bước 1, Kiểm tra mệnh đề $A(n)$ đúng với $n=p$
-Bước 2, giải thiết mệnh đề $A(n)$ đúng với số tự nhiên bất kì $n=k \geq p$ và phải chứng minh rằng nó cũng đúng với $n=k+1$
Trong hai bước trên:
- A. Chỉ có bước 1 đúng
- B. Chỉ có bước 2 đúng
- C. Cả hai bước đều đúng
- D. Cả hai bước đều sai
Câu 16: Cho dãy số $(u_{n})$ xác định bởi $u_{n} = n^{2} – 4n – 2$. Khi đó $u_{10}$ bằng:
- A. 48
- B. 60
- C. 58
- D. 10
Câu 17: Cho dãy số $u_{n} = 1+ (n +3).3^{n}$. khi đó công thức truy hồi của dãy là:
- A. $u_{n+1} = 1 +3u_{n} với $n≥1$
- B. $u_{n+1} = 1 +3u_{n} + 3^{n+1}$ với $n≥1$
- C. $u_{n+1} = u_{n} + 3^{n+1} - 2$ với $n≥1$
- D. $u_{n+1} =3u_{n} + 3^{n+1} - 2 với $n≥1$
Câu 18: Cho dãy số (v_{n}) xác định bởi :
Khi đó v11 bằng:
- A. 311
- B. 31024
- C. 332
- D. 322
Câu 19: Cho dãy số $u_{n} = n^{2} – 4n + 7$. Kết luận nào đúng?
- A. Dãy (u_{n}) bị chặn trên
- B. Dãy (u_{n}) bị chặn dưới
- C. Dãy (u_{n}) bị chặn
- D. Các mệnh đề A,B,C đều sai
Câu 20: Cho dãy số $z_{n} = 1 + (4n – 3).2n$
- A. Dãy $z_{n}$ là dãy tăng
- B. Dãy $z_{n}$ bị chặn dưới
- C. Cả A và B đề sai
- D. Cả A và B đều đúng