Trắc nghiệm Toán 8 chân trời sáng tạo bài tập cuối chương III

• A. $AB^{2}+BC^{2}=AC^{2}$

• B. $AB^{2}−BC^{2}=AC^{2}$
• C. $AB^{2}+AC^{2}=BC^{2}$
• D. $AB^{2}=AC^{2}+BC^{2}$

Câu 2: Một tam giác có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông

• A. 12 cm; 24 cm
• B. 10 cm; 22 cm

• C. 10 cm; 24 cm

• D. 15 cm; 24 cm

Câu 3: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH = 4cm, AB = 5cm. Tính BH

• A. 2 (cm)
• B. 5 (cm)

• C. 3 (cm)

• D. 4 (cm)

Câu 4: Cho hình vuông ABCD có cạnh bằng 4 cm. Tính độ dài đường chéo AC của hình vuông.

• A. AC=$\sqrt{32}$ cm

• B. AC=32 cm 
• C. AC=4 cm
• D. AC=16 cm

Câu 5: Cho tam giác ABC có 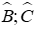 là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm; BH = 4,5cm; HC = 8cm. Khi đó ΔABC là tam giác gì?

• A. Tam giác cân

• B. Tam giác vuông

• C. Tam giác vuông cân
• D. Tam giác đều

Câu 6: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH = 4cm, AB = 5cm. Tính chu vi tam giác ABC

• A. 18 (cm)
• B. 15 (cm)

• C. 16 (cm)

• D. 20 (cm)

Câu 7: Chọn câu đúng nhất trong các câu sau khi định nghĩa tứ giác ABCD:

• A. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA

• B. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng

• C. Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó hai đoạn thẳng kề một đỉnh song song với nhau
• D.Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA và 4 góc tại đỉnh bằng nhau.

Câu 8: Tồn tại một tứ giác lồi có một góc:

• A.Bằng tổng ba góc kia 
• B.Lớn hơn tổng ba góc kia 
• C.Nhỏ nhất lớn hơn 90 độ

• D.Là góc tù

Câu 9: Trong tứ giác ABCD với đường chéo AC và BD cắt nhau tại O. $BO=4, OD=6,AO=8,OC=3$ và AB=6. Độ dài của AD là:

• A. $9$
• B. $10$
• C. $6\sqrt{3}$

• D. $\sqrt{166}$

Câu 10: Cho tứ giác ABCD, trong đó ?

• A. 220°

• B. 200°       
• C. 160°       
• D. 130°

 Câu 11: Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là 200°. Tổng số đo các góc ngoài tại 2 đỉnh A, C là:

• A. 160°         

• B. 260°         
• C. 180°        
• D. 100°

Câu 12: Tam giác ABC có  = 60°, các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc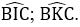 

• A. $\widehat{BIC}=100^{\circ}; \widehat{BKC}=80^{\circ}$
• B. $\widehat{BIC}=90^{\circ}; \widehat{BKC}=90^{\circ}$
• C. $\widehat{BIC}=60^{\circ}; \widehat{BKC}=120^{\circ}$

• D. $\widehat{BIC}=120^{\circ}; \widehat{BKC}=60^{\circ}$

Câu 13: Hình thang cân là hình thang có tính chất nào trong số các tính chất dưới đây? 

• A.   Có bốn cạnh song song với nhau.
• B.   Có hai đường chéo vuông góc với nhau.

• C.   Có hai góc kề một đáy bằng nhau.

• D.   Có bốn cạnh bằng nhau.

Câu 14: Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?

• A. Hình thang
• B. Hình thang vuông

• C. Hình thang cân

• D. Cả A, B, C đều sai

Câu 15: Một hình thang cân có cạnh bên là 2,5cm; đường trung bình là 3cm. Chu vi của hình thang là:

• A. 8cm
• B. 12cm
• C. 11cm

• D. 11,5cm

Câu 16: Cho hình thang cân MNPQ (MN // PQ) có góc MPQ = 45 độ và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:

• A. 418 $cm^{2}$

• B. 209 $cm^{2}$

• C. 290 $cm^{2}$
• D. 580 $cm^{2}$

Câu 17: Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và 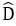 = 45° . Độ dài đáy lớn CD bằng

• A. 12cm         

• B. 16 cm         

• C. 18 cm         
• D. 20 cm

Câu 18: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:

• A. KI là đường trung trực của hai đáy AB và CD

• B. KI là đường trung trực của đáy AB nhưng không là đường trung trực của CD
• C. KI là đường trung trực của đáy CD nhưng không là trung trực của AB
• D. KI không là đường trung trực của cả hai đáy AB và CD.

Câu 19: Chọn đáp án đúng

• A. Hình bình hành có các cặp cạnh đối song song và bằng nhau.

• B. Hình bình hành có bốn cạnh bằng nhau.
• C. Hình bình hành và hình thoi đều có bốn góc bằng nhau.
• D. Hình bình hành có hai đường chéo bằng nhau.

Câu 20: Hãy chọn câu sai.

• A. Tứ giác có 4 cạnh bằng nhau là hình thoi
• B. Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi
• C. Hình bình hành có đường chéo là phân giác của một góc là hình thoi

• D. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi

Câu 21: Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là trung điểm của AE, EC, CF, FA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.

• A. Hình bình hành

• B. Hình thang vuông
• C. Hình thang cân
• D. Hình thang

Câu 22: Tỉ số độ dài hai cạnh của hình bình hành là 3 : 5. Còn chu vi của nó bằng 48cm. Độ dài cạnh kề của hình bình hành là:

• A. 12cm và 20cm
• B. 6cm và 10cm
• C. 3cm và 5cm

• D. 9cm và 15cm

Câu 23: Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?

• A. Tứ giác ABFE là hình bình hành
• B. EI là đường trung bình của tam giác ACD

• C. AI = ID

• D. Tứ giác EFCD là hình bình hành

Câu 24: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chọn khẳng định đúng.

• A. DE = FE; FE > FB

• B. DE = FE = FB

• C. DE > FE; EF = FB
• D. DE > FE > FB

Câu 25: Hãy chọn câu sai. Hình chữ nhật có

• A. Bốn góc                                         
• B. Hai đường chéo giao nhau tại trung điểm mỗi đường

• C. Hai đường chéo vuông góc với nhau

• D. Các cạnh đối bằng nhau

Câu 26: Hình vuông là tứ giác có

• A. Có bốn cạnh bằng nhau                

• B. Có bốn góc bằng nhau

• C. Có 4 góc vuông và bốn cạnh bằng nhau

• D. Cả A, B, C đều sai

Câu 27: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình gì?

• A. Hình chữ nhật

• B. Hình bình hành
• C. Hình thang cân
• D. Hình thang vuông

Câu 28: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?

• A. Hình chữ nhật

• B. Hình vuông

• C. Hình bình hành
• D. Hình thoi

Câu 29: Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:

• A. 16cm      
  

• B. 38cm          
• C. 18cm          
• D. 12cm

Câu 30: Cho hình chữ nhật ABCD có AB = a;AD = b. Cho M, N, P, Q là các đỉnh của tứ giác MNPQ và lần lượt thuộc các cạnh AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.

• A. $a^{2}+b^{2}$
• B. $\sqrt{a^{2}+b^{2}}$

• C. $2\sqrt{a^{2}+b^{2}}$

• D. $2(a^{2}+b^{2})$