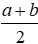Câu 1: Hãy chọn câu sai. Hình chữ nhật có
- A. Bốn góc
- B. Hai đường chéo giao nhau tại trung điểm mỗi đường
-
C. Hai đường chéo vuông góc với nhau
- D. Các cạnh đối bằng nhau
Câu 2: Hình vuông là tứ giác có
- A. Có bốn cạnh bằng nhau
-
B. Có bốn góc bằng nhau
-
C. Có 4 góc vuông và bốn cạnh bằng nhau
- D. Cả A, B, C đều sai
Câu 3: Hãy chọn câu sai.
-
A. Hình thang có một góc vuông là hình chữ nhật
- B. Hình bình hành có một góc vuông là hình chữ nhật
- C. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
- D. Hình thang cân có một góc vuông là hình chữ nhật
Câu 4: Khẳng định nào sau đây là sai?
- A. Hình vuông vừa là hình thoi vừa là hình chữ nhật
-
B. Hình vuông là hình chữ nhật nhưng không là hình thoi
- C. Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau
- D. Hình vuông có đường chéo là phân giác các góc trong hình vuông
Câu 5: Nếu ABCD là hình vuông thì:
- A. AC = BD
- B. AC, BD giao nhau tại trung điểm mỗi đường
- C. AC ⊥ BD
-
D. Cả A, B, C đều đúng
Câu 6: Hãy chọn câu sai. Cho ABCD là hình chữ nhật có O là giao điểm hai đường chéo. Khi đó
- A. AC = BD
- B. AB = CD; AD = BC
- C. AO = OB
-
D. OC > OD
Câu 7: Chọn câu đúng: Cho tứ giác ABCD có:
- A.
thì tứ giác ABCD là hình chữ nhật
- B. AB = CD; AC = BD thì tứ giác ABCD là hình chữ nhật
-
C. AB = BC; AD // BC, Â = 900 thì tứ giác ABCD là hình chữ nhật
- D. AB // CD; AB = CD thì tứ giác ABCD là hình chữ nhật
Câu 8: Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
- A. Hình vuông
- B. Hình thang cân
- C. Hình chữ nhật
-
D. Hình thoi
Câu 9: Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?
- A. Hình thoi
- B. Hình vuông
- C. Hình chữ nhật
-
D. Cả A và B
Câu 10: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình gì?
-
A. Hình chữ nhật
- B. Hình bình hành
- C. Hình thang cân
- D. Hình thang vuông
Câu 11: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
- A. Hình chữ nhật
-
B. Hình vuông
- C. Hình bình hành
- D. Hình thoi
Câu 12: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 5cm, 12cm là:
-
A. 6,5cm
- B. 6cm
- C. 13cm
- D. 10cm
Câu 13: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác 4 góc đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì?
- A. Hình chữ nhật
- B. Hình thoi
- C. Hình bình hành
-
D. Hình vuông
Câu 14: Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB. Tứ giác MNED là hình gì?
- A. Hình chữ nhật
-
B. Hình bình hành
- C. Hình thang cân
- D. Hình thang vuông
Câu 15: Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
- A. 4cm
-
B. 7 cm
- C. 14 cm
- D. 8 cm
Câu 16: Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
-
A. 16cm
- B. 38cm
- C. 18cm
- D. 12cm
Câu 17: Cho hình vuông có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông là:
-
A. 32
- B. 16
- C. 24
- D. 18
Câu 18: Cho tứ giác ABCD, lấy M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác ABCD cần có điều kiện gì để MNPQ là hình chữ nhật
- A. AB = BC
- B. BC = CD
- C. AD = CD
-
D. AC⊥ BD
Câu 19: Cho hình bình hành ABCD có AB = a, BC = b (a > b). Các phân giác trong của góc A, B, C, D tạo thành tứ giác MNPQ. Tính độ dài đường chéo của hình chữ nhật MNPQ theo a, b.
- A. QN = a – 2b
-
B. QN = a – b
- C. QN = a + b
- D. QN =
Câu 20: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.
-
A. BD ⊥ AC; BD = AC
- B. BD ⊥ AC
- C. BD = AC
- D. AC = BD và AB // CD
Câu 21: Cho hình chữ nhật ABCD có AB = a;AD = b. Cho M, N, P, Q là các đỉnh của tứ giác MNPQ và lần lượt thuộc các cạnh AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.
- A. $a^{2}+b^{2}$
- B. $\sqrt{a^{2}+b^{2}}$
-
C. $2\sqrt{a^{2}+b^{2}}$
- D. $2(a^{2}+b^{2})$
Câu 22: Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
-
A. M trên đường chéo AC
- B. M thuộc cạnh DC
- C. M thuộc đường chéo BD
- D. M tùy ý nằm trong hình vuông ABCD
Câu 23: Cho hình vuông có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông là:
- A. 32
-
B. 50
- C. 25
- D. 30
Câu 24: Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10. Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD. Tính độ dài các cạnh AB, AL, AK.
- A. $AB = 6; AL=5; AK=\sqrt{61}$
- B. $AB = 6; AL=\sqrt{52}; AK=4$
-
C. $AB = 6; AL=4; AK=\sqrt{52}$
- D. $AB = 4; AL=6; AK=\sqrt{52}$
Câu 25: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
-
A. M là hình chiếu của A trên BC
- B. M là trung điểm của BC
- C. M trùng với B
- D. Đáp án khác
- Câu 26: Cho hình cuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chọn câu đúng.
-
A. AK + CE = BE
- B. AK + CE = 2BE
- C. AK + CE = ½BE
- D. AK + CE > BE
Câu 27: Cho hình vuông ABCD cạnh 8 cm. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính diện tích tứ giác MNPQ.
- A. $S_{MNPQ}= 28cm^{2}$
- B. $S_{MNPQ}= 30cm^{2}$
- C. $S_{MNPQ}= 16cm^{2}$
-
D. $S_{MNPQ}= 32cm^{2}$
Câu 28: Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I. Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
-
A. Tam giác ABC vuông cân tại A
- B. Tam giác ABC vuông cân tại B
- C. Tam giác ABC đều
- D. Tam giác ABC vuông cân tại C
Câu 29: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Cho BC = 9 cm. Tính chu vi của tứ giác EFGH.
-
A. 12 cm
- B. 9 cm
- C. 16 cm
- D. 20 cm
Câu 30: Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E. Tìm vị trí điểm M để tứ giác ADME là hình vuông.
-
A. M là chân đường phân giác của  xuống cạnh BC.
- B. M là chân đường cao hạ từ đỉnh A xuống cạnh BC.
- C. M là chân đường trung tuyến từ đỉnh A xuống cạnh BC.
- D. Đáp án khác.