Bài 4: (3,5 điểm)
Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M; N lần lượt là điểm chính giữa của cung nhỏ AB; AC. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K.
a. Chứng minh tứ giác BMHI nội tiếp
b. Chứng minh MK.MN = MI.MC
c. Chứng minh tứ giác AKI cân tại K và tứ giác AHIK là hình thoi.
Bài Làm:
a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau 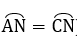
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b. Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau 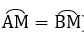
=> ΔMNI ∼ ΔMCK => $\frac{MN}{MC}=\frac{MI}{MK}$ => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau 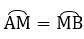
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
$\Rightarrow \left\{\begin{matrix}\widehat{KIN}=\widehat{ABN}& & \\ \widehat{BAC}=\widehat{IKC}& & \end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix}AH//KI& & \\ AK//HI& & \end{matrix}\right.$
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.

