Bài 4: (3,5 điểm)
Cho nửa đường tròn tâm O, đường kính AB = 2R. C là điểm nằm bất kì trên đường tròn sao cho C ≠A,B và AC < CB. D thuộc cung nhỏ BC sao cho ∠DOC = $90^{0}$. E là giao điểm của AD và BC; F là giao điểm của AC và BD
a. Chứng minh rằng tứ giác CEDF là tứ giác nội tiếp
b. Chứng minh rằng FC. FA = FD. FB
c. I là trung điểm của EF. Chứng minh rằng IC là tiếp tuyến của (O)
d. Khi C thay đổi thỏa mãn điều kiện của bài toán thì I thuộc đường tròn cố định nào?
Bài Làm:
Hình vẽ:

a. ∠ACB = $90^{0}$ (góc nội tiếp chắn nửa đường tròn)=>∠FCE = $90^{0}$
∠ADB = $90^{0}$ (góc nội tiếp chắn nửa đường tròn)=>∠FDE = $90^{0}$
Xét tứ giác CEDF có:
∠FCE = $90^{0}$
∠FDE = $90^{0}$
=> ∠FCE + ∠FDE = $180^{0}$
=> Tứ giác CEDF là tứ giác nội tiếp
b. Xét ΔAFD và ΔBFC có:
∠AFB là góc chung
∠ADF = ∠BCF = $90^{0}$
=> ΔAFD ∼ ΔBFC
=> $\frac{FA}{FB}=\frac{FD}{FC}$ => $FA.FC = FB.FD$
c. Do ∠FCE = $90^{0}$ Nên FE là đường kính đường tròn ngoại tiếp tứ giác CEDF
Do đó trung điểm I của FE là tâm đường tròn ngoại tiếp tứ giác CEDF
Tam giác CFI có IC = IF => ΔCFI cân tại I
=> CFI = ∠FCI
Tứ giác CEDF nội tiếp =>∠CFI = CDE (2 góc nội tiếp cùng chắn 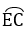
Tứ giác ACDB nội tiếp =>∠CDE = ∠CBA (2 góc nội tiếp cùng chắn 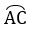
ΔAOB cân tại O =>∠BCO = ∠CBA
=> ∠FCI = ∠BCO
=> ∠FCI + ∠ECI = ∠BCO + ∠ECI <=> ∠FCE = ∠ICO
=> ∠ICO = $90^{0}$
Vậy IC là tiếp tuyến của (O)
d. Chứng minh tương tự câu c, ta có ∠IDO) = $90^{0}$
Xét tứ giác ICOD có:
∠ICO = ∠IDO = ∠COD = $90^{0}$
=> Tứ giác ICOD là hình chữ nhật
Lại có OC = OD = R
=> Tứ giác ICOD là hình vuông.
Có OI là đường chéo hình vuông cạnh R
=> OI = R√2
O cố định, do đó I thuộc đường tròn tâm O, bán kính R√2 cố định