Đề số 2: Đề kiểm tra toán 11 Kết nối bài Đường thẳng và mặt phẳng trong không gian (Đề tự luận)

I. DẠNG 1 – ĐỀ KIỂM TRA TRẮC NGHIỆM

ĐỀ 1

(Chọn chữ cái trước câu trả lời đúng nhất.)

Câu 1: Một mặt phẳng hoàn toàn được xác định nếu biếu điều nào sau đây?

• A. Ba điểm mà nó đi qua.
• B. Một điểm và một đường thẳng thuộc nó.
• C. Ba điểm không thẳng hàng.
• D. Hai đường thẳng thuộc mặt phẳng.

Câu 2: Trong các phát biểu sau, phát biểu nào đúng?

• A. Hình tứ diện có 4 cạnh.
• B. Hình tứ diện có 4 mặt.
• C. Hình tứ diện có 6 đỉnh.
• D. Hình tứ diện có 6 mặt.

Câu 3: Số cạnh của hình chóp tam giác là

• A. 5.
• B. 4.      
• C. 6.      
• D. 3.

Câu 4: Có duy nhất một mặt phẳng đi qua

• A. Hai đường thẳng.
• B. Một điểm và một đường thẳng.
• C. Ba điểm.
• D. Hai đường thẳng cắt nhau.

Câu 5: Có một và chỉ một mặt phẳng đi qua

• A. Ba điểm.
• B. Một điểm và một đường thẳng không chứa điểm đó.
• C. Hai điểm.
• D. Bốn điểm.

Câu 6: Hai đường thẳng chéo nhau nếu

• A. Chúng không có điểm chung.
• B. Chúng không cắt nhau và không song song với nhau.
• C. Chúng không cùng nằm trong bất kì một mặt phẳng nào.
• D. Chúng không nằm trong bất cứ hai mặt phẳng nào cắt nhau.

Câu 7: Thiết diện của mặt phẳng với tứ diện

• A. Tam giác hoặc tứ giác.
• B. Luôn là một tứ giác.
• C. Luôn là một tam giác.
• D. Tam giác hoặc tứ giác hoặc ngũ giác.

Câu 8: Cho 2 đường thẳng a,b cắt nhau và không đi qua điểm A. Xác định được nhiều nhất bao nhiêu mặt phẳng bởi a, b và A?

• A. 1.
• B. 2.
• C. 3.
• D. 4.

Câu 9: Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là

• A. 5 mặt, 5 cạnh.
• B. 6 mặt, 5 cạnh.
• C. 6 mặt, 10 cạnh.
• D. 5 mặt, 10 cạnh.

Câu 10: Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. số giao điểm của ba đường thẳng là

• A. 3.      
• B. 6.    
• C. 1.      
• D. Kết quả khác.

Xem lời giải

ĐỀ 2

(Chọn chữ cái trước câu trả lời đúng nhất.)

Câu 1. Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là

• A. 1.     
• B. 2.      
• C. 3.      
• D. 4.

Câu 2. Trong mặt phẳng cho tứ giác ABCD, điểm E∉. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm A,B,C,D,E?

• A. 6.
• B. 7.
• C. 8.
• D. 9.

Câu 3. Một hình chóp cụt có đáy là một n giác, có số mặt và số cạnh là 

• A. n+2 mặt, 2n cạnh.
• B. n+2 mặt, 3n cạnh.
• C. n+2 mặt, n cạnh.
• D. n mặt, 3n cạnh.

 Câu 4. Hình biểu diễn nào sau đây vẽ đúng hình chóp ?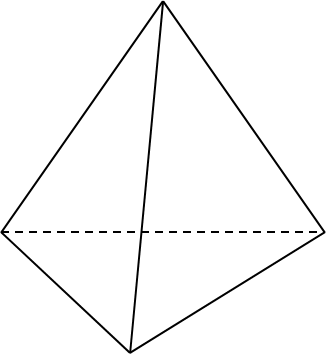 

A.	C.
B.	D.

Câu 5. Hình biểu diễn nào sau đây vẽ đúng hình hộp.

A.	C.
B.	D.

Câu 6. Trong phát biểu sau đây, phát biểu nào đúng?

• A. Hình chóp có tất cả các mặt là hình tam giác.
• B. Tất cả các mặt bên của hình chóp là hình tam giác.
• C. Tồn tại một mặt bên của hình chóp không phải là hình tam giác.
• D. Số cạnh bên của hình chóp bằng số mặt của nó.

Câu 7. Trong các phát biểu sau, phát biểu nào đúng?

• A. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
• B. Hai mặt phẳng có thể có đúng hai điểm chung.
• C. Nếu hai mặt phẳng có một điểm chung thì chúng có chung một đường thẳng duy nhất hoặc mọi điểm thuộc mặt phẳng này đều thuộc mặt phẳng kia.
• D. Hai mặt phẳng luôn có điểm chung. 

Câu 8. Cho hình tứ diện ABCD, phát biểu nào sau đây là đúng?

• A. AC và BD cắt nhau.
• B. AC và BD không có điểm chung.
• C. Tồn tại một mặt phẳng chứa AD và BC.
• D. AB và CD song song với nhau.

Câu 9. Chọn khẳng định sai trong các khẳng định sau?

• A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
• B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
• C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
• D. Nếu ba điểm phân biệt M,N,P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.

Câu 10. Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?

• A. Trong 4 điểm đã cho không có ba điểm nào thẳng hàng.
• B. Số mặt phẳng đi qua 3 trong 4 điểm đã cho là 4.
• C. Số đoạn thẳng nối hai điểm trong 4 điểm đã cho là 6.
• D. Trong 4 điểm đã cho luôn luôn tồn tại 3 điểm thuộc cùng 1 mặt phẳng.

Xem lời giải

II. DẠNG 2 – ĐỀ KIỂM TRA TỰ LUẬN

ĐỀ 1

Câu 1 (4 điểm). Cho hình chóp S.ABCD có  AC $\cap$ BD = M và  AB $\cap$ CD = N. Tìm giao tuyến của hai mặt phẳng 

a) SAC và SBD.

b) SAB và SCD.

Câu 2 (6 điểm).

a) Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho ? 

b) Trong mp ($\alpha$), cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Điểm S ∉ mp ($\alpha$). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên?

Xem lời giải

III. DẠNG 3 – ĐỀ TRẮC NGHIỆM VÀ TỰ LUẬN

ĐỀ 1

I. Phần trắc nghiệm (4 điểm)

(Chọn chữ cái trước câu trả lời đúng nhất.)

Câu 1. Cho hình chóp S.ABCDE như hình, phát biểu nào sau đây là đúng.

• A. Điểm B thuộc mặt phẳng (SAB).
• B. Điểm B thuộc mặt phẳng (SED).
• C. Điểm E thuộc mặt phẳng (SAB).
• D. Điểm D thuộc mặt phẳng (SBC).

Câu 2. Cho hình chóp S.ABCDE như hình vẽ, phát biều nào sau đây là đúng?

• A. SE và AB cắt nhau.
• B. SD và BC chéo nhau.
• C. Đường thẳng SB nằm trong mặt phẳng SED.
• D. (SAE) và (SBC) có một điểm chung duy nhất.

Câu 3.  Cho hình chóp S.ABCD có AC∩BD=M và AB∩CD=N. Giao tuyến của mặt phẳng SAC và mặt phẳng SBD là đường thẳng 

• A. SN.
• B. SC.
• C. SB.
• D. SM.

Câu 4. Cho hình chóp S.ABCD, O là giao điểm của AC và BD, phát biểu nào sau đây là đúng?

• A. Giao tuyến của (SAC) và (SBD) là SO.
• B. Giao tuyến của (SAB) và (SCD) là điểm S.
• C. Giao tuyến của (SBC) và (SCD) là SK, với K là giao điểm của SD và BC.
• D. Giao tuyến của (SOC) và (SAD) là SM, với M là giao điểm của AC và SD. 

II. Phần tự luận (6 điểm)

Câu 1 (3 điểm). Cho tứ diện ABCD. Gọi M, Nlần lượt là trung điểm AB và CD. Mặt phẳng ($\alpha$) qua MN cắt AD và BC lần lượt tại P, Q. Biết MP cắt NQ tại I. Chứng minh I, B, D thẳng hàng.

Câu 2 (3 điểm). Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SC, N là trên cạnh BC. Tìm giao điểm của đường thẳng SD với mặt phẳng AMN.

Xem lời giải

ĐỀ 2

I. Phần trắc nghiệm (4 điểm)

(Chọn chữ cái trước câu trả lời đúng nhất.)

Câu 1. Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?

• A. Giao điểm của (SMC) với BD là giao điểm của CN với BD, trong đó N là giao điểm của SM và AD.
• B. Giao điểm của (SAC) với BD là giao điểm của SA và BD.
• C. Giao điểm của (SAB) với CM là giao điểm của SA và CM.
• D. Đường thẳng DM không cắt mặt phẳng (SBC).

Câu 2. Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?

• A. Giao điểm của MN với (SBD) là giao điểm của MN với BD. 
• B. Đường thẳng MN không cắt mặt phẳng (SBD).
• C. Giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao điểm của CM với BD.
• D. Giao điểm của MN với (SBD) là M.

Câu 3. Cho tứ diện ABCD. G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng ACD và GAB là

• A. AM, M là trung điểm AB.
• B. AN, N là trung điểm CD.
• C. AH, H là hình chiếu của B trên CD.
• D. AK, K là hình chiếu của C trên BD.

Câu 4. Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?

• A. Thiết diện của (MND) với hình chóp là tam giác MND.
• B. Thiết diện của (MND) với hình chóp là tứ giác NDMB.
• C. Thiết diện của (MND) với hình chóp là tứ giác NDMK, với K là giao điểm của SB với NI, I là giao điểm của MD với BC.
• D. Thiết diện của (MND) với hình chóp là tam giác NDB.

II. Phần tự luận (6 điểm)

Câu 1 (3 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC. Gọi I là giao điểm của đường thẳng AM vơí mặt phẳng SBD. Khi đó tỉ số $\frac{MA}{IA}$ bằng bao nhiêu?

Câu 2 (3 điểm). Cho hình chóp S.ABCD, đáy ABCD là hình thang với AD là đáy lớn AD = 2BC, G là trọng tâm tam giác SCD. Mặt phẳng SAC cắt cạnh BG tại K. Khi đó, tỷ số $\frac{KB}{KG}$ bằng bao nhiêu?

Xem lời giải