Giá trị nhỏ nhất của biểu thức F = – 2x + y trên miền nghiệm của hệ bất phương trình

Bài 20 : Cặp số nào sau đây không là nghiệm của bất phương trình x – 2y ≥ 5?

A. (3; – 1).

B. (– 1; 4).

C. (2; – 3).

D. (1; – 2).

Xem lời giải

Bài 21 : Cặp số nào sau đây không là nghiệm của hệ bất phương trình 

x − 2y > 4 

2x + y > 6 

A. (2; – 1).

B. (7; 1).

C. (5; – 1).

D. (6; – 2).

Xem lời giải

Bài 22 : Phần không bị gạch (kể cả d) ở Hình 11 là miền nghiệm của bất phương trình:

A. 2x – 3y ≤ – 12.

B. 2x – 3y ≥ – 12.

C. 3x – 2y ≤ 12.

D. 3x – 2y ≥ 12.

Xem lời giải

Bài 23 : Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:

Xem lời giải

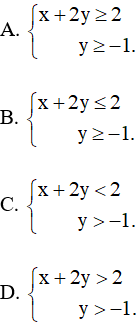
Bài 25 : Biểu diễn miền nghiệm của các bất phương trình sau:

a) 3x > 2;

b) 2y ≤ – 5;

c) 2x – y ≥ 1;

d) 3x – 2y < 5.

Xem lời giải

Bài 26 : Biểu diễn miền nghiệm của các hệ bất phương trình sau:

Xem lời giải

Bài 27 : 

a) Biểu diễn miền nghiệm của hệ bất phương trình 

3x − y ≤ 9 

3x + 6y ≤ 30

x ≥ 0                                (I). 

0 ≤ y ≤ 4 

b) Tìm x, y là nghiệm của hệ bất phương trình (I) sao cho F = 3x + 4y đạt giá trị lớn nhất.

Xem lời giải

Bài 28 : Một sân bóng đá được tổ chức tại một sân vận động có sức chứa 40 000 người, ban tổ chức phát hành hai loại vé là 400 000 đồng và 200 000 đồng. Do điều kiện sân đấu nên số lượng vé 400 000 đồng không lớn hơn số lượng vé 200 000 đồng. Để an toàn phòng dịch, liên đoàn bóng đá yêu cầu số lượng vé không vượt quá 30% sức chứa của sân. Để tổ chức được trận đấu thì số tiền thu được thông qua bán vé không được ít hơn 3 tỉ đồng. Gọi x, y lần lượt là số vé vé 400 000 đồng và 200 000 đồng được bán ra.

a) Viết hệ bất phương trình bậc nhất hai ẩn x, y để biển diễn số lượng vé mỗi loại được bán ra đảm bảo mục đích của ban tổ chức.

b) Chỉ ra hai nghiệm của hệ bất phương trình đó.

Xem lời giải

Bài 29 : Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ lắp ráp và 1 giờ để hoàn thiện; một chiếc ghế cần 1 giờ để lắp ráp và 2 giờ để hoàn thiện. Bộ phận lắp ráp có 3 nhân công, bộ phận hoàn thiện có 4 nhân công. Biết thị trường luôn tiêu thụ hết sản phẩm của xưởng và lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn.

a) Viết hệ bất phương trình mô tả số lượng bàn và ghế mà trong một ngày phân xưởng có thể sản xuất, biết một nhân công làm việc không quá 8 tiếng mỗi ngày.

b) Biểu diễn miền nghiệm của hệ bất phương trình đó.

c) Biết một chiếc bàn lãi 600 nghìn đồng, một chiếc ghế lãi 450 nghìn đồng. Hỏi trong một ngày, xưởng cần sản xuất bao nhiêu chiếc bàn, bao nhiêu chiếc ghế để thu được tiền lãi cao nhất.

Xem lời giải

Bài 30 : Hình 13 mô tả sơ đồ một sân khấu gắn với hệ trục tọa độ Oxy (đơn vị trên các trục tọa độ là 1 mét). Phần thính phòng giới hạn bởi hai đường thẳng d1 và d2 là vị trí ngồi của khán giả có thể nhìn thấy dàn hợp xướng. Gọi (x; y) là tọa độ ngồi của khán giả ở thính phòng. Viết hệ bất phương trình bậc nhất hai ẩn x, y mà khán giả có thể nhìn thấy dàn hợp xướng.

Xem lời giải